


Next: Espacios `` no homogéneos''.
Up: Operadores fraccionarios para medidas
Previous: Operadores fraccionarios para medidas
Supongamos que 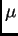 es una medida de Borel en el espacio métrico
es una medida de Borel en el espacio métrico
 a la que sólo le pedimos que sea finita sobre bolas y
que no tenga átomos. Estamos interesados en las propiedades de
acotación del operador integral
Supongamos que sabemos que este operador está acotado de
a la que sólo le pedimos que sea finita sobre bolas y
que no tenga átomos. Estamos interesados en las propiedades de
acotación del operador integral
Supongamos que sabemos que este operador está acotado de
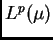 en
en  para unos ciertos
para unos ciertos
![$ p,q\in [1,\infty].$](img6.png) Sea
Sea 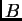 una bola abierta de radio
una bola abierta de radio  Entonces, para cada
Entonces, para cada 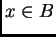 tenemos la estimación
Si esta estimación la combinamos con la acotación
tenemos la estimación
Si esta estimación la combinamos con la acotación
 que estamos suponiendo, resulta que
Esto sólo puede suceder para
que estamos suponiendo, resulta que
Esto sólo puede suceder para
 en cuyo caso obtenemos
Esta es la condición fundamental que les pediremos a las medidas,
lo que permitirá, en particular, que no sean doblantes. Así
llegamos a la noción de espacio `` no homogéneo'',
introducida por Nazarov, Treil y Volberg en [NTV1] y que
definimos en la sección siguiente.
Para que el núcleo de
en cuyo caso obtenemos
Esta es la condición fundamental que les pediremos a las medidas,
lo que permitirá, en particular, que no sean doblantes. Así
llegamos a la noción de espacio `` no homogéneo'',
introducida por Nazarov, Treil y Volberg en [NTV1] y que
definimos en la sección siguiente.
Para que el núcleo de  resulte localmente integrable
con respecto a
resulte localmente integrable
con respecto a 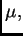 pediremos que
pediremos que 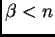 y pondremos
y pondremos
 Así tendremos que
Así tendremos que







